On this page

Advanced Scientific Plot Using Matplotlib

Jan 23, 2021

#python #numpy #matplotlib

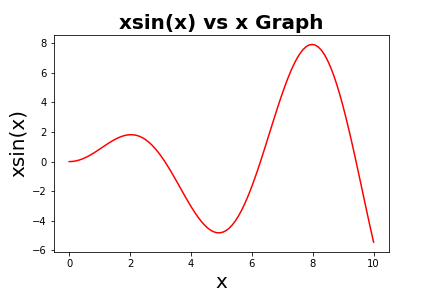
2D plot

First, We need to import the required modules for plotting. We write import numpy as np for including numerical python (numpy) package. Here we have shortened numpy as np which is the common short name. You can go with import numpy and for this case np will be replaced with numpy. Next we import matplotlib.pyplot package for plotting. Lines [4-5] for calculating data points. np.linspace() is a function that takes three arguments, first argument is the initial point, the second one for the final point, and third argument responsible for the no of data points equally spaced between initial and final points. plt.plot() function needs at least two arguments for two data points. Lines [7-11] are for decorating the plot.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0,10,100)
y = x*np.sin(x)

plt.plot(x,y,"r")
plt.xlabel('x',fontsize=20)
plt.ylabel("xsin(x)",fontsize=20)
plt.title("xsin(x) vs x Graph",fontsize=20,weight="bold")
plt.savefig("2d-plot.png")
plt.show()
2dplot

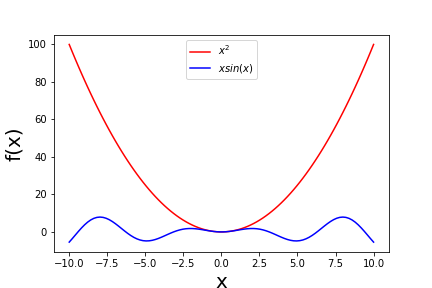
Multi plot

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10,10,100)
y1 = x**2
y2 = x*np.sin(x)

plt.plot(x,y1,'r',label=r"$x^2$")
plt.plot(x,y2,'b',label=r"$xsin(x)$")

plt.xlabel("x",fontsize=20)
plt.ylabel("f(x)",fontsize=20)
plt.legend(loc="best")
plt.savefig("demo2.png")
plt.show()
multi-plot

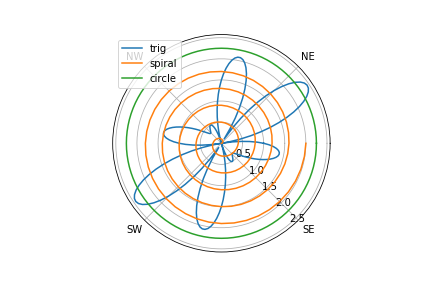
Polar plot

import numpy as np
import matplotlib.pyplot as plt
pi=np.pi
theta = np.linspace(0,2*pi,201)
r1 = np.abs(np.cos(5.0*theta)-1.5*np.sin(3.0*theta))
r2 = theta/pi
r3 = 2.25*np.ones_like(theta)
plt.ion()

plt.polar(theta,r1,label='trig')
plt.polar(5*theta,r2,label='spiral')
plt.polar(theta,r3,label='circle')

plt.thetagrids(np.arange(45,360,90),('NE','NW','SW','SE'))
plt.rgrids((0.5,1.0,1.5,2.0,2.5),angle=310)
plt.legend(loc='best')
plt.savefig("polar-plot.png")
plt.show()
polar-plot

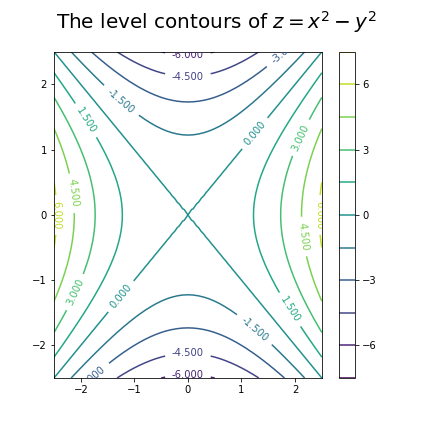
Contour plot

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm

[X,Y] = np.mgrid[-2.5:2.5:51j,-2.5:2.5:61j]
Z = X**2 - Y**2

curves=plt.contour(X,Y,Z,10)
plt.colorbar()
plt.clabel(curves)

plt.suptitle(r'The level contours of $z=x^2-y^2$',fontsize=20)
plt.show()
contour-plot

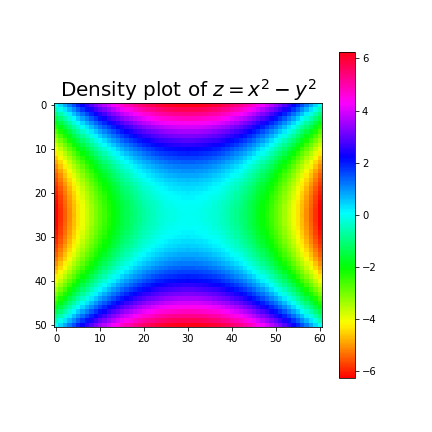
Density plot

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm

plt.ion()
[X,Y] = np.mgrid[-2.5:2.5:51j,-2.5:2.5:61j]
Z = X**2 - Y**2

plt.figure()
plt.imshow(Z,cmap=cm.hsv)
plt.colorbar()
plt.title(r'Density plot of $z=x^2-y^2$',fontsize=20)
plt.show()
density-plot

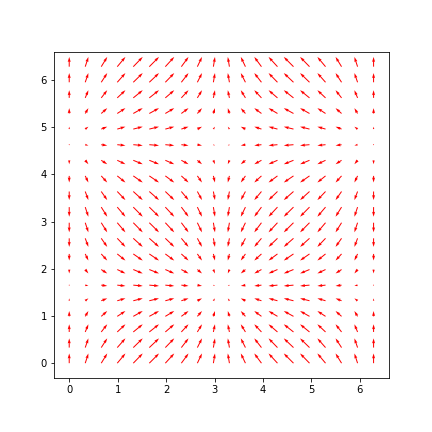
Vector plot

import numpy as np
import matplotlib.pyplot as plt
from pylab import rcParams
rcParams['figure.figsize'] = 6,6

x,y = np.meshgrid(np.linspace(0,2*np.pi,20),np.linspace(0,2*np.pi,20))
u = np.sin(x)
v = np.cos(y)

plt.streamplot(x,y,u,v)
plt.show()
vector-plot

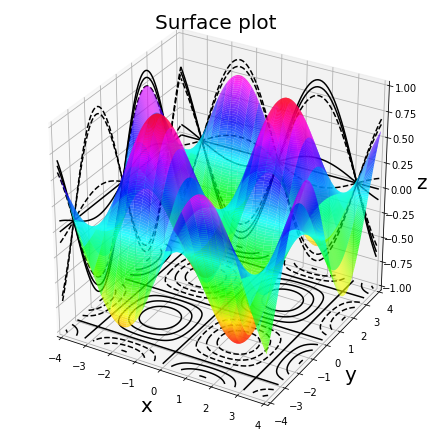
3D surface plot

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.cm as cm

plt.ion()
fig = plt.figure()
ax = Axes3D(fig)

[x,y] = np.mgrid[-4:4:101j,-4:4:1011j]

z = np.sin(x)*np.sin(y)
ax.plot_surface(x,y,z,rstride=4,cstride=3,color='c',alpha=0.8,cmap=cm.hsv)
#ax.plot_wireframe(x,y,z,rstride=4,cstride=3) #for wireframe plot
ax.contour(x,y,z,zdir='x',offset=-4,colors='black')
ax.contour(x,y,z,zdir='y',offset=4,colors='black')
ax.contour(x,y,z,zdir='z',offset=-1,colors='black')

ax.set_xlabel("x",fontsize=20)
ax.set_ylabel("y",fontsize=20)
ax.set_zlabel("z",fontsize=20)

ax.set_xlim3d(-4,4)
ax.set_ylim3d(-4,4)
ax.set_zlim3d(-1,1)

ax.set_title("Surface plot",fontsize=20)
plt.savefig("demo11.png")
plt.show()
surface-plot